- در این جلسه، ما یک پایه محکم برای سیستم اعداد و توابع ریاضی ایجاد خواهیم کرد. با کمک مثال های واقعی کار، ما سر خود را پیرامون موضوعاتی مانند اعداد مختلط، مختصات دکارتی و قطبی، نگاشت توابع ریاضی در ابعاد مختلف و درون یابی با موارد استفاده از آنها در موشن گرافیک و ساختمان سایه بان قرار می دهیم.
- معرفی
- سیستم شماره
- آشنایی مختصر با اعداد مختلط
- مقدمه ای بر توابع ریاضی
- جبر توابع
- ترکیب تابع
- از موارد برخی از توابع رایج استفاده کنید
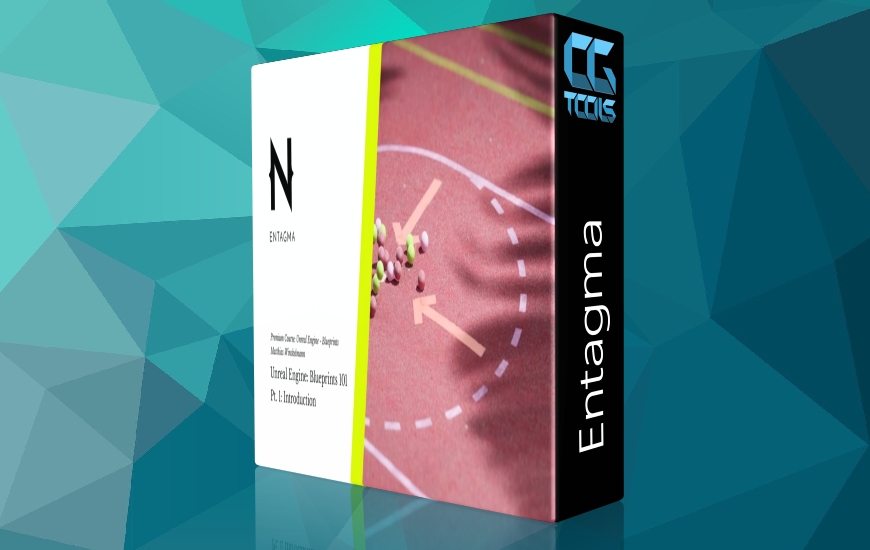
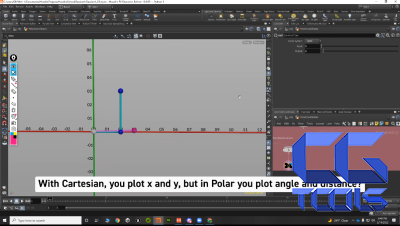
- مختصات کارتزین
- توسعه ذهنیت برای تبدیل فضا با استفاده از مختصات قطبی
- درون یابی خطی و گام صاف
- جلسه تمرین گروهی
- در این جلسه با بردارها آشنا می شویم. وکتورها یکی از مفاهیم مهم در گرافیک کامپیوتری هستند. آنها بلوکهای سازنده بیشتر قطعات گرافیکی متحرک دو بعدی و سه بعدی هستند. ما راه های مختلفی را مورد بحث قرار خواهیم داد که در آنها می توانیم از بردارها برای حل مسئله و جهت دهی هنری استفاده کنیم. ما همچنین به طور خلاصه به موضوعاتی از حساب چند متغیره نگاه خواهیم کرد تا بینش هایی در زمینه های برداری به دست آوریم.
- مقدمه ای بر وکتورها
- نقطه در مقابل جهت
- بزرگی و جهت بردارها
- وضوح وکتور
- جبر بردارها
- محصول نقطه ای
- محصول متقابل
- فیلدهای برداری
- واگرایی و پیچش
- بردارهای گرادیان
- جلسه تمرین گروهی
- در این جلسه با کواترنیون ها کار می کنیم و اهمیت آنها را در مورد چرخش های اویلر مورد بحث قرار می دهیم. از طریق این جلسه، ما یک رابطه بین کواترنیون ها و اعداد مختلط ایجاد می کنیم که می تواند برای اشکال زدایی الگوریتم های مبتنی بر کواترنیون ما مفید باشد. ما یاد خواهیم گرفت که چگونه می توان از آنها برای چرخاندن اشیاء در فضای سه بعدی استفاده کرد و به ما کمک کرد تا بر برخی از محدودیت های ماتریس ها غلبه کنیم.
- مقدمه ای بر کواترنیون ها
- زوایای اویلر در مقابل کواترنیون ها
- رابطه بین کواترنیون ها و اعداد مختلط
- چرخش سه بعدی با استفاده از کواترنیون ها
- زوایای اویلر به کواترنیون ها
- کواترنیون به زوایای اویلر
- ماتریس کواترنیون به چرخش
- درون یابی کواترنیونی
- سایر توابع مفید کواترنیون
- جلسه تمرین گروهی
- در این جلسه از آنچه تاکنون آموخته ایم برای درک مفهوم ماتریس استفاده خواهیم کرد. ما در مورد نیاز به ماتریس ها و موارد استفاده از آنها بحث خواهیم کرد. ما همچنین به فرآیند بستهبندی تبدیلها به یک ماتریس و سپس باز کردن بستهبندی برای انواع موارد استفاده خواهیم کرد. به طور کلی، ما سعی خواهیم کرد با درک ریاضی و مفهومی ماتریس ها با استفاده از آنها راحت باشیم.
- مقدمه ای بر ماتریس ها
- ضرب ماتریس
- باز کردن بسته بندی ماتریس
- بردارهای پایه
- سیستم های مختصات استوانه ای و کروی
- تبدیل با استفاده از ماتریس
- کواترنیون ها و ماتریس ها
- درون یابی ماتریسی
- موارد استفاده از ماتریس ها در گرافیک کامپیوتری
- خلاصه

این دوره ضبط شده راهی را برای هنرمندان فراهم می کند تا با استفاده از برنامه ها و روش های استاندارد صنعت، شهودی را برای استفاده از ابزارهای ریاضی در کار خود بیاموزند و توسعه دهند. این دوره نه تنها راههای استفاده از ریاضیات در هودینی را نشان میدهد، بلکه بر توسعه ذهنیتی برای حل مسائل جدید با استفاده از ریاضیات تمرکز میکند. دانشآموزان همچنین نکات و ترفندهای مرتبط با ریاضی را برای بهینهسازی پروژههای از پیش رندر شده یا بلادرنگ خود یاد خواهند گرفت.
دانشآموزان این کلاس را با درک اساسی از روشهای مختلف استفاده از ابزارهای ریاضیات برای موشن گرافیک، ساختمان سایهبان و برنامهنویسی گیمپلی ترک خواهند کرد. دانش آموزان یاد خواهند گرفت که برخی از تنظیمات موجود خود را با استفاده از ریاضیات بهینه کنند.
جلسه 1 : درک توابع و سیستم اعداد
جلسه 2 : درک بردارها
جلسه 3 : درک کواترنیون ها
جلسه 4 : درک تبدیل ماتریس ها